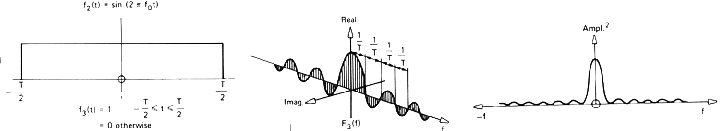Fourier Transform¶
Recap¶
- What is a complex number?
- What is the trigonometric form of a complex number?
- What is the difference between the cartesian and polar coordinate system?
- How to compute $r$ and $\varphi$ using $\Re$ and $\Im$ and vice versa?
Euler formula¶
\begin{equation} z=\Re + i\cdot\Im \\ z=A\cdot(\cos{\varphi} + i\cdot\sin{\varphi})\\ e^{ix}=\cos{x}+i\sin{x} \\ z=A\cdot e^{i\varphi} \end{equation}Taylor series¶
\begin{equation} f(x) = f(a) + \frac{f'(a)}{1!} (x-a) + \frac{f''(a)}{2!} (x-a)^2 + \frac{f'''(a)}{3!} (x-a)^3 +\ldots \end{equation}\begin{equation} f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x-a)^n \end{equation}- where $f^{(0)}(x)=f(x)$ and $0!=1$
- for $a=0$ also known as Maclaurin series
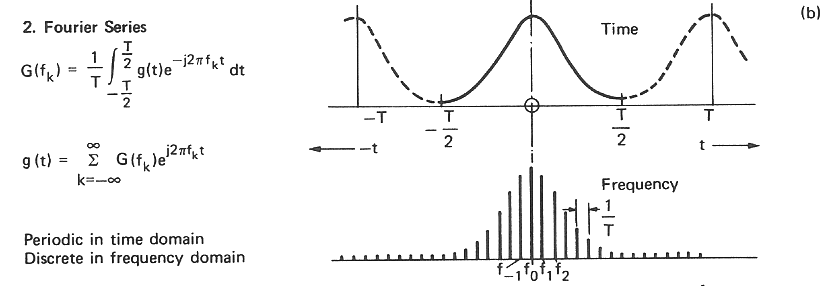
Fourier series¶
- for orthogonal functions $g_1\ldots g_n$ and coefficients $a_1\ldots a_n$ let us define:
- let us take $g_1$ use it to multiply both sides of the above equation:
- let us also compute the integral of both sides of the equation:
Fourier series¶
- because all the components are orthogonal their products are always 0,
- we can therefore remove most of the equation:
- to compute the coefficient $a_1$ we can simply use:
- we can use a similar equation for all other coefficients:
Trigonometric Fourier series¶
- Fourier used $\sin$ as the $g_n$ function:
(where $\omega_0=\frac{2\pi}{T_0}=2\pi f_0$ - ie. angular frequency, with unit rad/s)
- We can use the following equations:
- To simplify the computation like this:
Trigonometric Fourier series¶
\begin{equation} f(t) = a_0 + \sum_{n=1}^{\infty}a_n\cdot\cos(n\omega_0t)+b_n\cdot\sin(n\omega_0t) \end{equation}- where $a_n$ and $b_n$ are known as the Fourier coefficients:
Complex Fourier series¶
- We use the complex version of the Fourier formula more often:
- where $F_n$ is computed:
Properties¶
\begin{equation} a_n=2\Re[F_n] \quad b_n=-2\Im[F_n] \end{equation}\begin{equation} F_0=a_0 \end{equation}\begin{equation} F_{-n}=F_n^{*} \quad |F_n|=|F_{-n}| \quad \angle(F_n)=-\angle(F_{-n}) \end{equation}(Hermitian symmetry)
\begin{equation} a_n=(F_n+F_{-n}) \quad b_n=i\cdot(F_n-F_{-n}) \end{equation}\begin{equation} F_n=0.5\cdot(a_n-i\cdot b_n) \quad F_{-n}=0.5\cdot(a_n+i\cdot b_n) \end{equation}\begin{equation} A_n=\sqrt{a_n^2+b_n^2}=2|F_n| \end{equation}Fourier transform¶
\begin{equation} F_n=\frac{1}{T_0}\int_{0}^{T_0}f(t)\cdot e^{-in\omega_0t}\ dt \end{equation}Fourier series is defined only for periodic signals (with the period $T_0$)!
How can we compute the Fourier series for non-periodic signals?
Given that $\omega_0=\frac{2\pi}{T_0}=2\pi f_0$
If $T_0\rightarrow\infty$ then $\omega_0\rightarrow0$
Thus the $F_n$ coeffients will turn from a series of points $\rightarrow$ function of real values $F(\xi)$
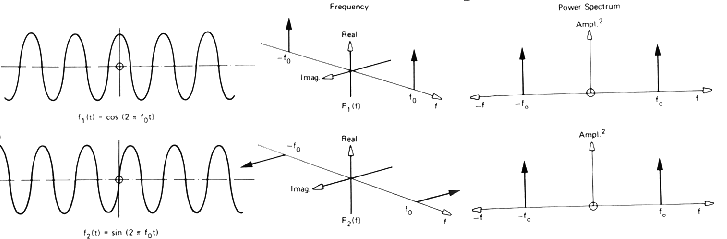
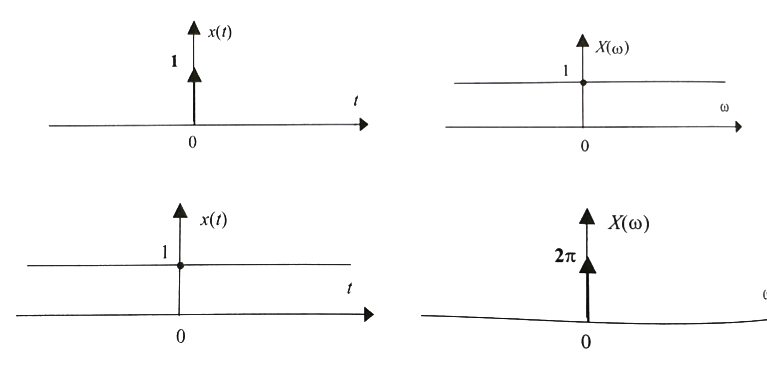
Fourier transform¶
- Analitic function
- Synthetic function (aka. invrerse):
- Apart from the decomposition in the frequency domain, other useful forumlas include:
- Amplitude spectrum: $|F(\xi)|$
- Phase spectrum: $\angle[F(\xi)]$
- Power spectrum: $|F(\xi)|^2$
When is it computable?¶
- finite energy: $\int_{-\infty}^{\infty}\lvert x(t) \rvert^2dt<\infty$
- finite number of extrema
- finite number of discontinuities
- any periodic signal (including inifinite energy)
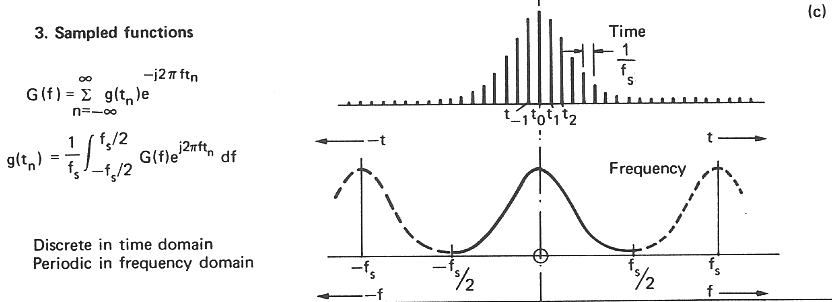
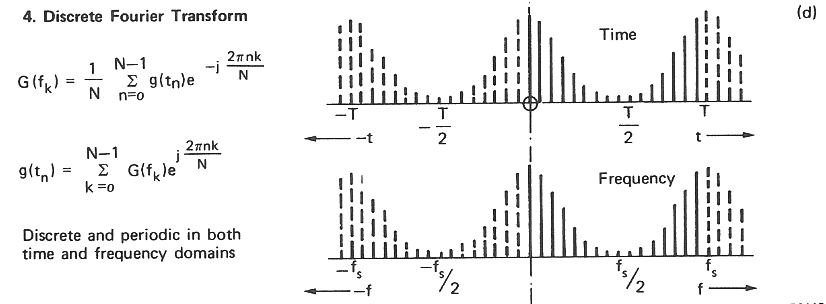
Discrete Fourier transform¶
Used for digital signals
Analitic function:
- Synthetic function (inverse):
Types of Fourier transforms¶
Fourier series¶
DTFT¶
DFT¶
Properties of the Fourier transform¶
\begin{equation} f(t) \qquad\rightarrow\qquad F(\omega) \end{equation}Inverse¶
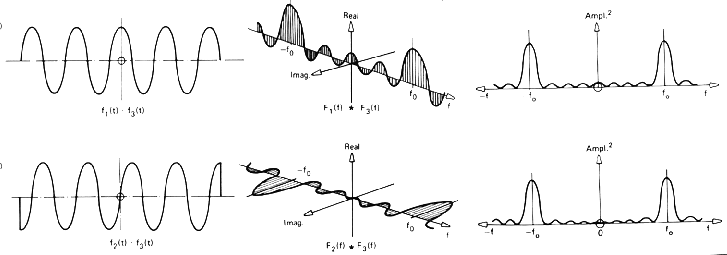
\begin{equation} F(t) \qquad\rightarrow\qquad 2\pi f(-\omega) \end{equation}Convolution¶
\begin{equation} f_1\star f_2(t) \qquad\rightarrow\qquad F_1(\omega)F_2(\omega) \end{equation}Product¶
\begin{equation} f_1(t)f_2(t) \qquad\rightarrow\qquad \frac{1}{2\pi}F_1\star F_2(\omega) \end{equation}Shift¶
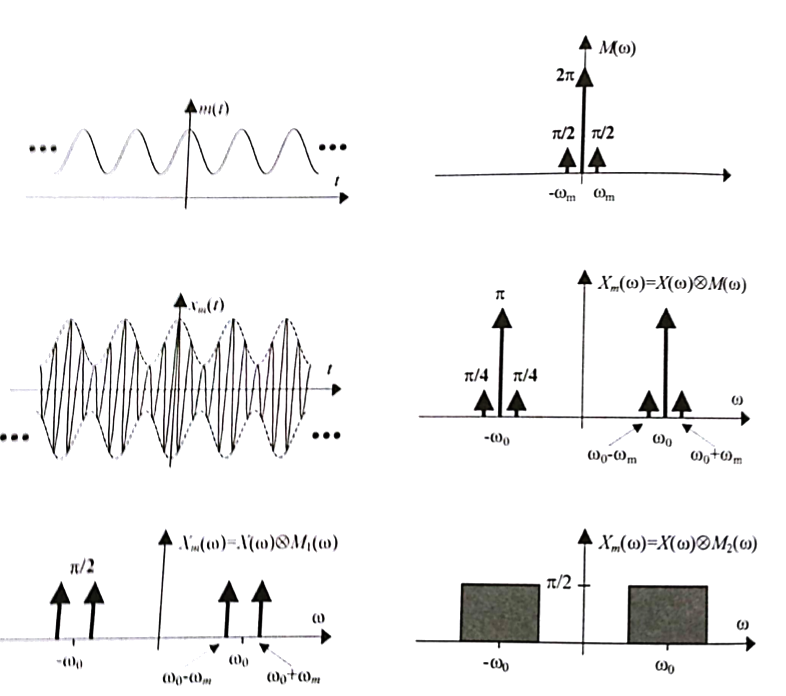
\begin{equation} f(t-u) \qquad\rightarrow\qquad e^{-iu\omega}F(\omega) \end{equation}Amplitude modulation¶
\begin{equation} e^{i\xi t}f(t) \qquad\rightarrow\qquad F(\omega-\xi) \end{equation}Scaling¶
\begin{equation} f(t/s) \qquad\rightarrow\qquad |s|F(s\omega) \end{equation}Time derivative¶
\begin{equation} f^{(p)}(t) \qquad\rightarrow\qquad (i\omega)^{(p)}F(\omega) \end{equation}Frequency derivative¶
\begin{equation} (-it)^{(p)}f(t) \qquad\rightarrow\qquad F^{(p)}(\omega) \end{equation}Complex conjugation¶
\begin{equation} f^{\star}(t) \qquad\rightarrow\qquad F^{\star}(-\omega) \end{equation}Hermitian symmetry¶
\begin{equation} f(t)\in \mathbb{R} \qquad\rightarrow\qquad F(-\omega)=F^{\star}(\omega) \end{equation}A bit more on symmetry¶
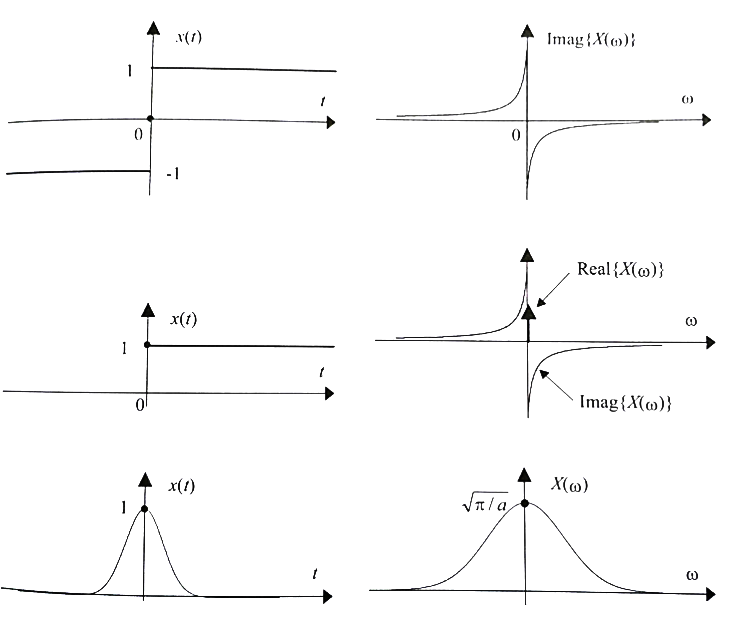
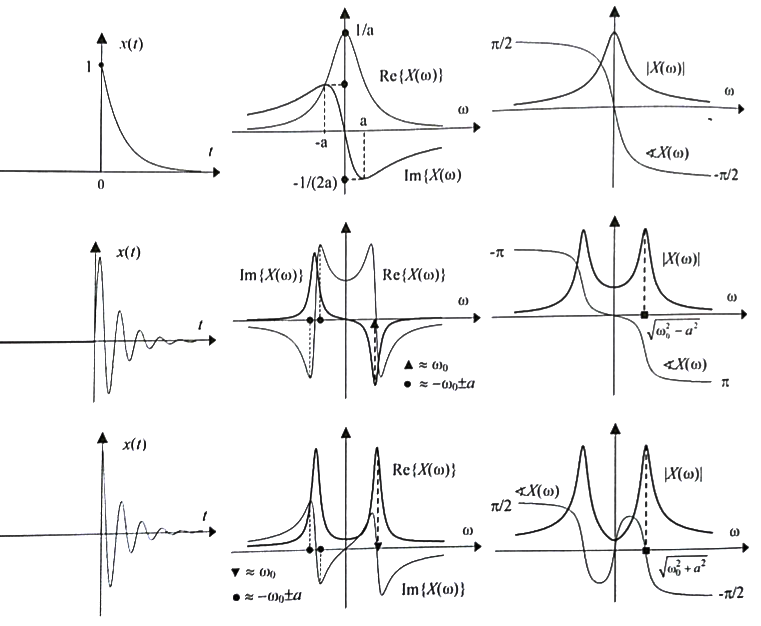
- for any real signal $f(t)$, Fourier transform has the following properties:
- $\Re(F)$ - is an even function
- $\Im(F)$ - is an odd function
- $\lvert F \rvert$ - is an even function
- $\angle(f)$ - is an odd function
- if $X$ isn't symmetric as above, FT isn't a real function (it's complex)
- additionally:
- if $f(t)$ is real and even - $F(\omega)$ is also real and even
- if $f(t)$ is real and odd - $F(\omega)$ is completely imaginary and odd
- since every singal can be decomposed into its even and odd part:
- the even component of $f(t)$ corresponds to the $\Re[F(\omega)]$
- the odd component of $f(t)$ corresponds to $i\Im[F(\omega)]$
Parseval theorem¶
\begin{equation} \int_{-\infty}^{\infty}f(x)g^{*}(x)\ dx=\int_{-\infty}^{\infty}F(\xi)G^{*}(\xi)\ d\xi \end{equation}Plancherel theorem¶
\begin{equation} \int_{-\infty}^{\infty}||f(x)||^2\ dx=\int_{-\infty}^{\infty}||F(\xi)||^2\ d\xi \end{equation}- Signal power:
- For discrete signals:
Examples¶