Literatura¶
- Zieliński T. Cyfrowe przetwarzanie sygnałów WKiŁ. 2005-7.
- Lyons R.G. Wprowadzenie do cyfrowego przetwarza-nia sygnałów WKiŁ. 1999.
- Szabatin J. Podstawy teorii sygnałów WKiŁ. 1982.
- Szabatin J. Przetwarzanie sygnałów (online) 2003.
- Damian Karwowski Zrozumieć Kompresję Obrazu (online) 2019.
Ćwiczenia:
- José Unpingco Python for Signal Processing Springer 2013.
- Allen B. Downey Think DSP: Digital Signal Processing in Python, O'Reily, 2016.
Warunki zaliczeń¶
Ćwiczenia¶
- Każde ćwiczenie jest oceniane od 2-5
- Ocena końcowa to średnia wszystkich ćwiczeń
- Nieoddane lub niezaliczone ćwiczenie to ocena 0
- Ćwiczenia oddajemy najpóźniej na następnej lekcji
- W uzasadnionych przypadkach można poprosić o przedłużenie terminu oddania
- Dozwolone maksymalne 2 nieobecności na ćwiczeniach bez uzasadnienia (1 na stud. zaocznych)
Egzamin¶
- Egzamin dotyczy materiału z wykładów
- Pytania będą dotyczyły zarówno definicji pojęć, jak i rozwiązywaia prostych zadań
Wprowadzenie¶
- Sygnał to ogólnie wszelki umowny znak o treści informacyjnej
- łac. signum $\rightarrow$ znak
- czas. sygnalizować

- Dla nas to przede wszystkim przebieg zmiennośći pewnego zjawiska (zwykle w czasie)
- Używamy do:
- badania zjawisk fizycznych i systemów
- sterowania systemami
- przekazywania informacji
Dyskusja¶
Podaj przykłady sygnałów występujących w świecie?
- naturalne?
- sztuczne?
- do sterowania?
- do transmisji informacji?
Obszary użycia przetwarzania sygnałów¶
- telekomunikacja
- transmisja informacji, elektronika
- dźwięk, muzyka, obraz, multimedia
- astronomia
- medycyna
- radary
- nawigacja satelitarna
- zjawiska fizyczne (np. sejsmologia, meteorologia)
- analiza danych numerycznych (np. rynkowych)
Przetwarzanie sygnałów¶
- Synteza lub generowanie sygnałów
- Analiza lub parametryzacja sygnałów
- Modyfikacja - przetwarzanie sygnałów
Transmisja sygnału¶
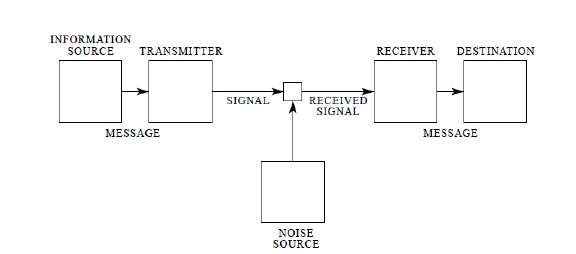 (Shannon i Weaver, 1948)
(Shannon i Weaver, 1948)
Rodzaje sygnału¶
- funkcja czasu, położenia, ...
- $f(t)$ lub $f(x)$
- jednowymiarowe lub dwuwymiarowe lub wielowymiarowe
- $f(x)$ lub $f(x,y)$
- rzeczywiste lub zespolone
- $\mathbb{R}$ lub $\mathbb{C}$
- ciągłe lub dyskretne (analogowe lub cyfrowe)
- deterministyczna lub losowe
- okresowe, impulsowe, nieskończone
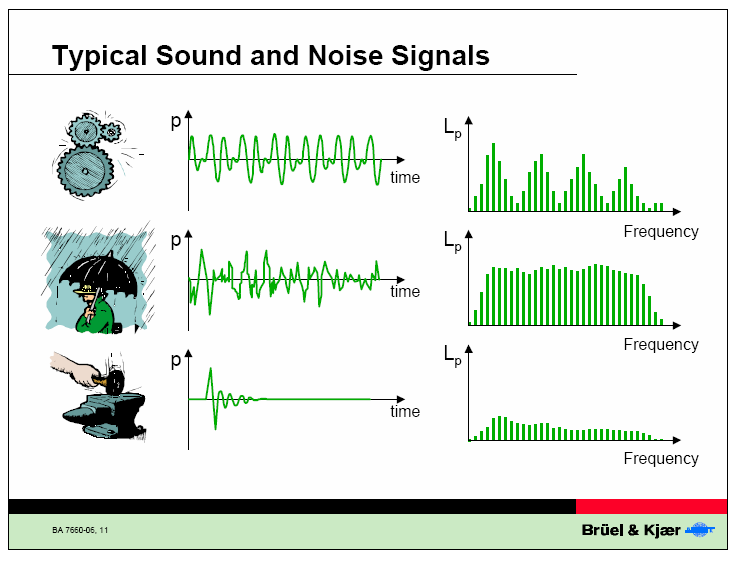
(T. Zieliński)
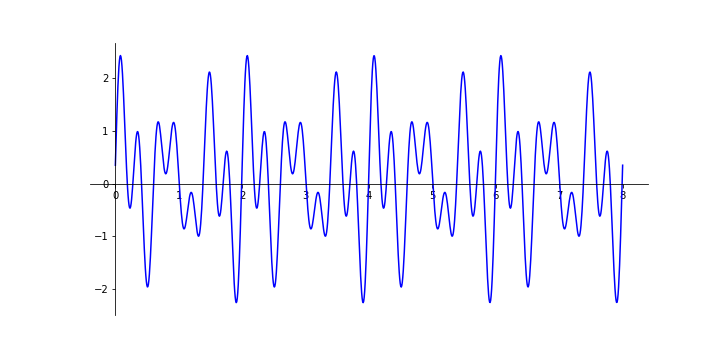
Sygnały okresowe¶
Sygnał okresowy (ang. periodic) to taki w którym:
- istnieje wartość $T$, zwana okresem sygnału
- dla której, dla wszystkich wartości czasu $t \in \mathbb{R}$ i dla dowolnej liczby $k \in \mathbb{Z}$ zachodzi zależność:
$x(t)=x(t+kT)$
Przykłady sygnałów deterministycznych¶
- Impuls prostokątny

Przykłady sygnałów deterministycznych¶
- Skok jednostkowy
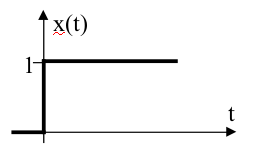
Przykłady sygnałów deterministycznych¶
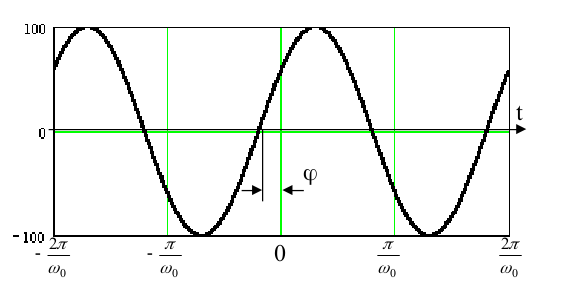
- Sygnał sinusoidalny
\begin{equation}
x(t)=A\sin(\omega_0t+\phi)
\end{equation}
Przykłady sygnałów deterministycznych¶
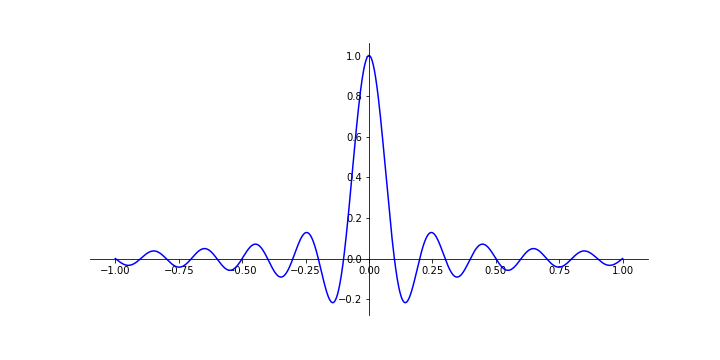
- Sinc (w uproszczeniu)
\begin{equation}
x(t)=\frac{\sin(\omega_0t)}{\omega_0t}
\end{equation}
Sygnały losowe¶
- stacjonarne - parametry statystycznie nie zmieniają się w czasie
- ergodyczne - parametry statystyczne również niezmienne dla dowolnej realizacji procesu losowego w dowolnej chwili w czasie
- ergodyczne procesy losowe zazwyczaj aproksymujemy używając dystrybucji statystycznej, np:
- równomierna (ang. uniform)
- normalna (ang. normal, Gaussian)
- Poissona
- itd...

(T. Zielinski)
Reprezentacja sygnału¶
- sygnał najczęściej zapisujemy jako funkcję wartości rzeczywistych w czasie: $f(x)$
- sygnał może jednak być reprezentowany jako funkcja liczb zespolonych
- przykładem sygnału zespolonego to przebieg wykładniczy:
- sygnały można też przeskształcać do innych dziedzin
- przykładowo za pomocą transformaty Fouriera do dziedziny częstotliowści
Sygnał cyfrowy¶
- Sygnał ciągły (analogowy)
- Sygnał dyskretny czasu ciągłego
- np. wyjście DAC przed filtrowaniem
- kwantyzacja
- Sygnał ciągły czasu dyskretnego
- np. wyjście matrycy CCD
- dyskretyzacja (próbkowanie)
- Sygnał dysktretny czasu dyskretnego - sygnał cyfrowy
Zalety cyfrowego przetwarzania danych¶
- programowalność, elastyczność
- stabilność, odporność na zakłócenia, starty
- powtarzalność
- kompresja danych
- wydajna praca wielokanałowa
- niska cena
Transformaty¶
- sygnał jest reprezentowany za pomocą funkcji operującej na liczbach, np:
- transformata to działanie matematyczne (podobne do funkcji) ale operujące na funkcjach:
- pozwalają "inaczej spojrzeć" na zawartość sygnału
- znacznie upraszczają niektóre działania matematyczne
Rozkład przedmiotu¶
- Przetwarzanie sygnałów jedno-wymiarowych
- Sygnały i ich parametry
- Systemy LTI i splot
- Transformata Fouriera
- Kwantyzacja i kodowanie sygnału
- Dyskretna transformata Fouriera, FFT, STFT
- Filtry cyfrowe
- Przetwarzanie obrazów
- Kodowanie obrazu, przestrzenie barw
- Histogramy i transformacje punktowe
- Splot w obrazie
- Transformaty w obrazie
- Operacje morfologiczne
- Podsumowanie i powtórzenie materiału